Using ConvexPoly.osax
The ConvexPoly.osax dictionary can be opened in a script editor. The dictionary displays all available commands and the definitions of various objects such as planes (half spaces) and polyhedra. Built-in polyhedra are obtained by executing:
set poly to platonic polyhedron 2 -- 1 to 5. The 5 Platonic solids.
set poly to archimedean polyhedron 2 -- 1 to 13. The 13 Archimedean solids.
set poly to catalan polyhedron 2 -- 1 to 13. The duals of the Archimedean solids.
These commands return records which describe the polyhedra (see below).
Platonic solids are numbered :
1 Cube, 2 Octahedron, 3 Tetrahedron, 4 Icosahedron, 5 Dodecahedron.
Archimedean solids are numbered :
1 CubeOctahedron, 2 Great Rhombicosidodecahedron, 3 Great Rhombicuboctahedron, 4 Icosidodecahedron, 5 Small Rhombicosidodecahedron, 6 Small Rhombicuboctahedron, 7 Snub Cube, 8 Snub Dodecahedron, 9 Truncated Cube, 10 Truncated Dodecahedron, 11 Truncated Icosahedron, 12 Truncated Octahedron, 13 Truncated Tetrahedron.
Catalan solids are numbered :
1 Rhombic Dodecahedron, 2 Disdyakis Triacontahedron, 3 Disdyakis Dodecahedron, 4 Rhombic Triacontahedron, 5 Deltoidal Hexecontahedron, 6 Deltoidal Icositetrahedron, 7 Pentagonal Icositetrahedron, 8 Pentagonal Hexecontahedron, 9 Triakis Octahedron, 10 Triakis Icosahedron, 11 Pentakis Dodecahedron, 12 Tetrakis Hexahedron, 13 Triakis Tetrahedron.
Platonic and Archimedean polyhedra are inscribed in the sphere of radius scale centered at the origin. Catalan solids are tangent to the same sphere. The optional parameter scale defaults to 100 and may be used to get coordinates suitable for drawing in a window or for any other purpose.
For instance:
set poly to platonic polyhedron 2 -- the Octahedron
-- {plane list:{{normal:{-0.57735026919, -0.57735026919, -0.57735026919}, cst:57.735026918963}, {normal:{-0.57735026919, -0.57735026919, 0.57735026919}, cst:57.735026918963}, {normal:{-0.57735026919, 0.57735026919, -0.57735026919}, cst:57.735026918963}, {normal:{-0.57735026919, 0.57735026919, 0.57735026919}, cst:57.735026918963}, {normal:{0.57735026919, -0.57735026919, -0.57735026919}, cst:57.735026918963}, {normal:{0.57735026919, -0.57735026919, 0.57735026919}, cst:57.735026918963}, {normal:{0.57735026919, 0.57735026919, -0.57735026919}, cst:57.735026918963}, {normal:{0.57735026919, 0.57735026919, 0.57735026919}, cst:57.735026918963}}, vertex list:{{0.0, 0.0, 100.0}, {100.0, 0.0, 0.0}, {0.0, 100.0, 0.0}, {0.0, 0.0, -100.0}, {0.0, -100.0, 0.0}, {-100.0, 0.0, 0.0}}, facet list:{{5, 4, 6}, {1, 5, 6}, {4, 3, 6}, {3, 1, 6}, {2, 4, 5}, {1, 2, 5}, {2, 3, 4}, {2, 1, 3}}, name:"Octahedron"}
The object polyhedron contains a list of planes, a list of vertices and a list of facets. A plane contains a normal and a cst. It defines the set of points x such that normal.x = cst and by extension the half space defined by normal.x ≤ cst. For instance:
set poly to platonic polyhedron 2 scale 1
set p to item 1 of plane list of poly
-- {normal:{-0.57735026919, -0.57735026919, -0.57735026919}, cst:0.57735026919}
normal of p
-- {-0.57735026919, -0.57735026919, -0.57735026919}
cst of p
-- 0.57735026919
Vertices are obtained as follows:
set poly to platonic polyhedron 2
item 1 of vertex list of poly
-- {0.0, 0.0, 100.0}
Facets are obtained as follows:
set poly to platonic polyhedron 2
item 1 of facet list of poly
-- {5, 4, 6}
This facet is the triangle made by items 5, 4 and 6 of vertex list of poly. Facets are ordered is the same way as planes, i.e. item 5 of facet list of poly is the facet contained in the plane item 5 of plane list of poly.
You may construct your own polyhedron by providing a list of vertices or a list of planes.
For instance you provide a list of vertices to get the convex hull of these vertices:
set vlist to {{0, 0, 0}, {1, 0, 0}, {0, 1, 0}, {0, 0, 1}} -- a simplex
set poly to convex polyhedron with vertices vlist
-- {plane list:{{normal:{0.57735026919, 0.57735026919, 0.57735026919}, cst:0.57735026919}, {normal:{-1.0, 0.0, 0.0}, cst:0.0}, {normal:{0.0, -1.0, 0.0}, cst:0.0}, {normal:{0.0, 0.0, -1.0}, cst:0.0}}, vertex list:{{0.0, 0.0, 0.0}, {1.0, 0.0, 0.0}, {0.0, 1.0, 0.0}, {0.0, 0.0, 1.0}}, facet list:{{3, 2, 4}, {1, 3, 4}, {2, 1, 4}, {1, 2, 3}}}
Or you provide a list of planes (half spaces) to get the intersection, if any, of these half spaces:
set plist to {{normal:{0.0, 0.0, -1.0}, cst:0.0}, {normal:{0.0, -1.0, 0.0}, cst:0.0}, {normal:{-1.0, 0.0, 0.0}, cst:0.0}, {normal:{0.57735026919, 0.57735026919, 0.57735026919}, cst:0.57735026919}}
set poly to convex polyhedron with planes plist
-- {plane list:{{normal:{0.0, 0.0, -1.0}, cst:0.0}, {normal:{0.0, -1.0, 0.0}, cst:0.0}, {normal:{-1.0, 0.0, 0.0}, cst:0.0}, {normal:{0.57735026919, 0.57735026919, 0.57735026919}, cst:0.57735026919}}, vertex list:{{0.0, 0.0, 1.0}, {0.0, 1.0, 0.0}, {1.0, 0.0, 0.0}, {0.0, 0.0, 0.0}}, facet list:{{3, 2, 4}, {1, 3, 4}, {2, 1, 4}, {1, 2, 3}}}
Notice that vertex list of poly or plane list of poly may be empty if the provided data are inconsistent.
Polyhedra may be rotated, translated and scaled. For instance:
set poly to platonic polyhedron 1
set poly to rotate polyhedron poly axis {0, 0, 1} angle pi / 2
set poly to translate polyhedron poly vector {0, 0, 100}
set poly to scale polyhedron poly scale 1/100
The intersection of convex polyhedra is a convex polyhedron. It may be obtained as follows:
set poly1 to platonic polyhedron 1
set poly2 to platonic polyhedron 2
set poly3 to platonic polyhedron 3
set poly123 to intersect polyhedra {poly1,poly2,poly3}
You can get the 2D projection of a polyhedron using project2D. The direct object of project2D is a polyhedron or a list of vertices. The required parameters are an eye position, e.g. {0,1,0} and an up vector, e.g. {0,0,1}. For instance:
set poly to platonic polyhedron 1 scale 100
set poly2D to project2D poly eye position {3, 2, 1} up {0, 0, 1}
-- {facet list:{{1, 2, 3, 4}, {5, 6, 2, 1}, {1, 4, 7, 5}}, edge list:{{1, 2}, {2, 3}, {3, 4}, {4, 1}, {5, 6}, {6, 2}, {1, 5}, {4, 7}, {7, 5}}, vertex list:{{16.012815380509, 34.236839400873}, {80.064076902544, 59.914468951528}, {-16.012815380509, 77.032888651964}, {-80.064076902544, 51.35525910131}, {16.012815380509, -77.032888651964}, {80.064076902544, -51.35525910131}, {-80.064076902544, -59.914468951528}}}
vertex list of poly2D are 2D vectors and facet list contains the list of visible facets. You may call project2D with two boolean optional parameters planes and hidden. With planes poly2D also contains the list of visible planes; with hidden poly2D contains an additional list hidden facet list of hidden facets and (with planes and hidden) a list hidden plane list of the hidden planes.
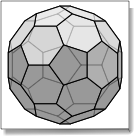
Viewing convex polyhedra
The script editor Smile contains extensions such as Graphic Library with which you can easily create graphic windows and display geometric data in PDF format. The following script displays a platonic polyhedron.
set poly to platonic polyhedron 4 scale 150 --icosahedron
set poly2D to project2D poly eye position {2, 2, 1} up {0, 0, 1}
set w to BeginFigure(0)
SetTransformation({1, 0, 0, 1, 200, 200}) --center the drawing in the window
repeat with f in facet list of poly2D
set l to {}
repeat with i in f
set end of l to item i of vertex list of poly2D
end repeat
MoveTo(item 1 of l)
LineTo(l)
ClosePath()
end repeat
SetFillColor({0.7, 0.7, 0.7})
DrawPath(3)
EndFigure()
set name of w to name of poly
See the samples for more examples.
The Samples folder contains a dialog Display polyhedron which helps drawing a convex polyhedon.
Using references
In the above sections you get a polyhedron as a record of type polyhedron. If you ask for further computations on the same polyhedron, the record is sent to ConvexPoly.osax which recalculates the polyhedron for internal use. Alternately you may ask for a polyhedron as polyhedron reference with the command
set poly to platonic polyhedron 1 as polyhedron reference
In that case the internal representation of poly is kept in memory so that further computations with poly won't require its calculation. This may speed up your script. You may obtain the record representation with
set polyrecord to poly as polyhedron
If you don't use poly anymore you should run the following command in order to free the memory used by poly:
delete polyhedron poly
|